Answer:
(x+2)(2x+2) = 130
x=6.58m
Explanation:
The shape of the whole figure is a triangle. Hence the area of the whole figure is expressed as:
Area = Length * Width
Given
Length = 2 + x + x = 2+2x
Width = 2 + x
Area = 130m²
Substitute the resultng values into the formula;
(2+2x)(2+x)= 130
(x+2)(2x+2) = 130
Expand the bracket:
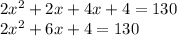
Divide through by 2
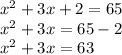
Complete the square by adding the square of the half of the coefficient of x to both sides:
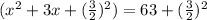
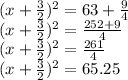
Take the square root of both sides
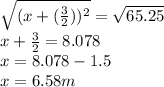
Hence the value of x is 6.58m