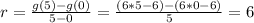Answer:
Here we can only answer A and B.
For a given function f(x), the average rate of change in a given interval [a, b] is given by:
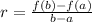
A) we have g(x) = 14*x + 6, and the interval [0, 5], the average rate of change is:
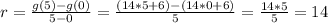
The average rate of change is 14.
B) We have g(x) = 3*(2x) - 6
we can rewrite this as:
g(x) = 3*2*x - 6 = 6x - 6
And we want to find the rate of change in the interval [0, 5]
is: