Question

If the temperature of a volume of dieal gas ncreases for 100 to 200, what happens to the average kinetic energy of the molecules?

Answer 1

It increases but less than double

Step-by-step explanation:

As the temperature of a gas increase, the average kinetic energy of the gas increases. The kinetic energy of a gas is the thermal energy that the gas contains.

We know, the kinetic energy of an ideal gas is given by :

`$V_(avg) = \sqrt{(8R)/(\pi M)}$`

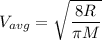
where, R = gas constant

T = absolute temperature

M = molecular mass of the gas

From the above law, we get

`$V_(avg) \propto √(T)$`

Thus, if we increase the temperature then the average kinetic energy of the ideal gas increases.

In the context, if the temperature of the ideal gas increases from 100°C to 200°C, then

`$((V_(avg)_2))/((V_(avg)_1)) =\sqrt{(T_2)/(T_1)}$`

`$((V_(avg)_2))/((V_(avg)_1)) =\sqrt{(473.15)/(373.15)}$`

`$((V_(avg)_2))/((V_(avg)_1)) =√(1.26)$`

`$((V_(avg)_2))/((V_(avg)_1)) =1.12$`

`$(V_(avg))_2 = 1.12\ (V_(avg))_1$`

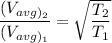
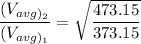
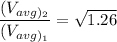
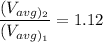
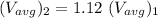
Therefore,
`$(V_(avg))_2 > (V_(avg))_1$`

Thus the average kinetic energy of the molecule increases but it increases 1.12 times which is less than the double.

Thus, the answer is " It increases but less that double".