Answer:
The manufacturer should advertise 11720 pages.
Explanation:
Normal Probability Distribution
Problems of normal distributions can be solved using the z-score formula.
In a set with mean
 and standard deviation
and standard deviation
 , the z-score of a measure X is given by:
, the z-score of a measure X is given by:

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
Mean of 12450, standard deviation of 570:
This means that
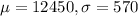
How many pages should the manufacturer advertise for each cartridge if it wants to be correct 90 percent of the time?
They should advertise the 10th percentile, which is X when Z has a p-value of 0.1, so X when Z = -1.28. Then

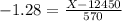
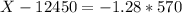
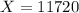
The manufacturer should advertise 11720 pages.