Solution :
Given data:
Mean, μ = $87,500
Standard deviation, σ = $26,000
Sample number, n = 63
a). The value of
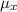 :
:
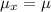
= 87,500
b). The value of
 :
:
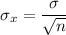

= 3275.69
c). The shape of the sampling distribution is that of a normal distribution (bell curve).
d). The value z-score for the value =80,000.
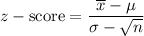

= -2.2896
≈ -2.29
e). P(x > 80000) = P(z > -2.2896)
= 0.9890