Question

What is the dimensionless heat conduction rate for a sphere at surface temperature T1 buried in an infinite medium of temperature T2?a. 2*D.b. 2.34*D.c. Pi*D.d. 5.93*D.

Answer 1

The dimensionless conduction heat rate,
`$q_(ss)^*$`

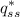
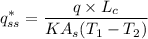`$q_(ss)^*=(q* L_c)/(K A_s(T_1-T_2))$` ...........(1)

where
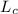`$L_c$` = characteristic length

`$=\left((A)/(4\pi) \right)^(1/2). \sqrt{(D^2)/(4)}$`

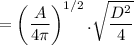
A is surface area

q = heat transfer

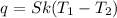`$q=Sk(T_1-T_2)$` ..................(2)

where, S = conductor shape factor

Now substituting (2) in (1),

`$q_(ss)^* = (Sk(T_1-T_2)L_c)/(kA(T_1-T_2))$`

`$q_(ss)^* = (S * L_c)/(A)$`

`$q_(ss)^* = (S * D/2)/(\pi D^2)$`

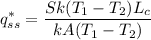
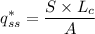
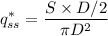
`$q_(ss)^* = (S * D)/(2\pi D^2)$` ...................(3)

For a sphere, we know S = 2πD

Putting this in (3),

`$q_(ss)^* = (2 \pi D * D)/(2\pi D^2)$`

`$q_(ss)^* = (2 \pi D^2)/(2\pi D^2)$`

`$q_(ss)^* = 1$`

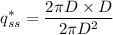
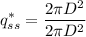
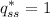
Therefore, the dimensionless heat conduction rate for a sphere is 1.