Question

The volume of a cylinder is given by the formula V=πr^2h, where r is the radius of the cylinder and h is the height. Which expression represents the volume of this cylinder?

h=2x+7
r=x-3

Options:
1: 2πx^3 - 12πx^2 - 24πx + 63π
2: 2πx^3 - 5πx^2 - 24πx + 63π
3: 2πx^3 + 7πx^2 - 18πx - 63π
4: 2πx^3 + 7πx^2 + 18πx + 63π

Images for more detail:

Answer 1

B

Explanation:

We are given a cylinder with a height of (2x + 7) and a radius of (x - 3).

And we want to find the expression for the volume of the cylinder.

Recall that the volume of a cylinder is given by:

`\displaystyle V = \pi r^2 h`

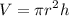
Where r is the radius and h is the height.

Substitute:

`\displaystyle V = \pi(x-3)^2(2x+7)`

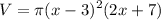
Expand. We can use the perfect square trinomial pattern:

`\displaystyle V = \pi \left[\underbrace{(x^2-6x+9)}_((a-b)^2=a^2-2ab+b^2)(2x+7)\right]`

Distribute:

`V=\pi \left[ 2x(x^2-6x+9)+7(x^2-6x+9)\right]`

Distribute:

`V = \pi \left[(2x^3-12x^2+18x)+(7x^2-42x+63)\right]`

Rewrite:

`V = \pi\left[(2x^3)+(-12x^2+7x^2)+(18x-42x)+(63)\right]`

Combine like terms:

`V = \pi (2x^3-5x^2-24x+63)`

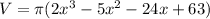
Distribute:

`V = 2\pi x^3-5\pi x^2 -24\pi x+63\pi`

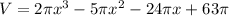
Hence, our answer is B.