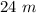Question

One of the diagonals of a rhombus of perimeter 120m is 36m. Find its area and the length of the other diagonal. pls answer fasttt

Answer 1

Answer:
`864\ m^2,\ 24\ m`

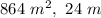
Explanation:

Given

Perimeter of the rhombus is
`120\ m`

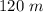
Length of one of the diagonal is
`d_1=36\ m`

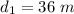
All the sides of the rhombus are equal

`\Rightarrow 4a=120\\\Rightarrow a=30\ m`

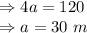
Area of the rhombus with side and one diagonal is

`\Rightarrow \text{Area=}(1)/(2)d√(4a^2-d^2)`

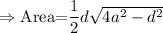
Insert the values

`\Rightarrow \text{Area=}(1)/(2)* 36* √(4\cdot 30^2-36^2)\\\\\Rightarrow \text{Area= }18√(3600-1296)\\\Rightarrow \text{Area= }18* 48\\\Rightarrow \text{Area= }864\ m^2`

Area with two diagonals length can be given by

`\Rightarrow \text{Area =}0.5* d_1* d_2 \\\text{Insert the values}\\\Rightarrow 864=36* d_2\\\Rightarrow d_2=24\ m`

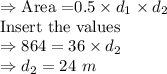
Thus, the area of the rhombus is
`864\ m^2` and the length of the other diagonal is
`24\ m`