Answer:
x = 6
Explanation:
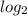 ( x + 5 ) +
( x + 5 ) +
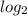 ( ( x - 5 ) =
( ( x - 5 ) =
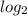 11
11
Determined the define range.
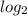 ( x + 5 ) +
( x + 5 ) +
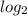 ( ( x - 5 ) =
( ( x - 5 ) =
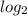 (11), x ∈ ( 5, + ∞ )
(11), x ∈ ( 5, + ∞ )
We know that
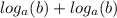 =
=
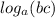
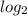 ( x + 5 ) ( x - 5 ) =
( x + 5 ) ( x - 5 ) =
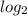 ( 11).
( 11).
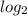 ( ( x + 5 ) × ( x - 5 ) ) =
( ( x + 5 ) × ( x - 5 ) ) =
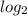 ( 11).
( 11).
Use indentity :- ( a + b ) ( a - b ) = a² - b².
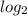 ( x² + 25) =
( x² + 25) =
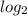 ( 11).
( 11).
Since , the base of the logarithm are the same. set the arguments equal.
x² - 25 = 11.
Move constant to the right-hand side and change their sign.
x² = 11 + 25
x² = 36.
Take square root of each side.
√x² = √36
x = ± 6
x = 6
x = -6, x ∈ ( 5, + ∞ )
Check if the solutions is in determine range.
x = 6