Question

An artificial satellite circling the Earth completes each orbit in 125 minutes. (a) Find the altitude of the satellite.(b) What is the value of g at the location of this satellite?

Answer 1

(a) Altitude = 1.95 x 10⁶ m = 1950 km

(b) g = 5.9 m/s²

Step-by-step explanation:

(a)

The time period of the satellite is given by the following formula:

`T^2 = (4\pi^2r^3)/(GM_E)`

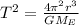
where,

T = Time period = (125 min)(
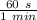`(60\ s)/(1\ min)`) = 7500 s

r = distance of satellite from the center of earth = ?

G = Universal Gravitational Constant = 6.67 x 10⁻¹¹ N.m²/kg²

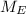`M_E` = Mass of Earth = 6 x 10²⁴ kg

Therefore,

`(7500\ s)^2 = (4\pi^2r^3)/((6.67\ x\ 10^(-11)\ N.m^2/kg^2)(6\ x\ 10^(24)\ kg))\\\\r^3 = ((7500\ s)^2(6.67\ x\ 10^(-11)\ N.m^2/kg^2)(6\ x\ 10^(24)\ kg))/(4\pi^2)\\\\r = \sqrt[3]{5.7\ x\ 10^(20)\ m^3} \\`

r = 8.29 x 10⁶ m

Hence, the altitude of the satellite will be:

`Altitude = r - radius\ of\ Earth\\Altitude = 8.29\ x\ 10^6\ m - 6.34\ x\ 10^6\ m`

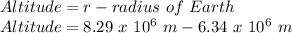
Altitude = 1.95 x 10⁶ m = 1950 km

(b)

The weight of the satellite will be equal to the gravitational force between satellite and Earth:

`Weight = Gravitational\ Force\\\\M_sg = (GM_EM_s)/(r^2)\\\\g = (GM_E)/(r^2)\\\\g = ((6.67\ x\ 10^(-11)\ N.m^2/kg^2)(6\ x\ 10^(24)\ kg))/((8.23\ x\ 10^6\ m)^2)`

g = 5.9 m/s²