Question

Male Color Blindness When conducting research on color blindness in males, a researcher forms random groups with five males in each group. The random variable x is the number of males in the group who have a form of color blindness (based on data from the National Institutes of Health).X Px0 0.6591 0.2872 0.0503 0.0044 0.0015 0+In determine whether a probability distribution is given. If a probability distribution is given, find its mean and standard deviation. If a probability distribution is not given, identify the requirements that are not satisfied.

Answer 1

The sum of the probabilities of all possible outcomes is not 1, which means that a probability distribution is not given.

Explanation:

We are given these following probabilities:

`P(X = 0) = 0.6591`

`P(X = 1) = 0.2872`

`P(X = 2) = 0.0503`

`P(X = 3) = 0.0044`

`P(X = 4) = 0.0015`

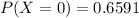
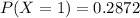
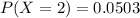
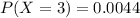
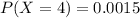
Determine whether a probability distribution is given.

We have to see if the sum of the probabilities of all possible outcomes is 1. So

`0.6591 + 0.2872 + 0.0503 + 0.0044 + 0.0015 = 1.0025`

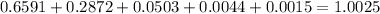
The sum of the probabilities of all possible outcomes is not 1, which means that a probability distribution is not given.