Question

Two people start from the same point. One walks east at 4 mi/h and the other walks northeast at 8 mi/h. How fast is the distance between the people changing after 15 minutes?

Answer 1

5.89 mi/h

Explanation:

This problem can be solved by using different methods. I will use vectors since it's the simplest way in which we can solve it. This can be solved by using related rates of change though.

First, we start by drawing a diagram with the velocity vectors.

A= velocity of the first person

B= velocity of the second person

C= velocity in which they are moving away from each other.

Since there is no acceleration in the problem, we can suppose we are talking about constant speeds, so the velocity at which they are moving away from each other will always remain constant. (It doesn't matter what time it is, the velocity will always be the same)

Having said this we can solve this problem by using the components, by using law of cosines or graphically. I will use law of cosines. The idea is to find the length of side c.

Law of cosines:

`C^(2)=A^(2)+B^(2)-2ABcos \gamma`

so we can solve the formula for C so we get:

`C=\sqrt{A^(2)+B^(2)-2ABcos \gamma}`

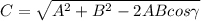
and now we can substitute the values we know:

`C=\sqrt{(4)^(2)+(8)^(2)-2(4)(8)cos 45^(o)}`

`C=\sqrt{16+64-32√(2)}`

`C=\sqrt{80-32√(2)} mph`

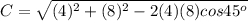
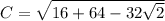
if we want an exact answer, then that will be the exact answer, which approximates to:

C=5.89 mph