Question

Find the common ratio for this geometric sequence.

72, 12, 2, 1/3, 1/18

OA. 1/3
ОВ. 1/6
OC. 3
OD. 6

Answer 1

1/6

Explanation:

We need to find the common ratio for the given Geometric Series . We know that ,

Geometric Series:- When a common number is multiplied to each term to obtain the next term of the Series is called Geometric Series .

Common Ratio :- The number which is multiplied to obtain the next term of the series .

Here the given series is ,

`\rm\implies Series = 72 , 12 , 2 , (1)/(3),(1)/(18)`

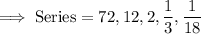
We can find the common ratio by dividing the consecutive terms , As ,

`\rm\implies Common \ Ratio (r) = ( n \ th \ term )/( ( n - 1)th \ term )`

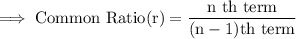
Substitute the respective values ,

`\rm\implies Common \ Ratio (r) = ( 12 )/( 72 )`

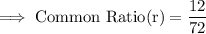
Simplify by dividing the term in RHS ,

`\rm\implies \boxed{\blue{\rm Common \ Ratio (r) = ( 1 )/( 6 ) }}`

Hence the common ratio is 1/6 .