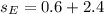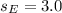Question

Question

Elvira and Aletheia live 3.2 miles apart on the same street. They are in a study group that meets at a coffee shop between their houses. It took Elvira 1/2 hour and Aletheia 2/3 hour to walk to the coffee shop. Find both women's walking speeds.

Answer 1

Missing from the question

Aletheia's speed is 0.6 miles per hour slower than Elvira's speed.

Answer:

`s_E = 3.0`

`s_A = 2.4`

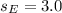
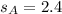
Explanation:

Given

`d = 3.2m` -- distance

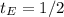`t_E = 1/2` --- Elvira time

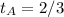`t_A = 2/3` --- Aletheia time

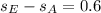`s_E - s_A = 0.6` --- the relationship between their speeds

Required

Their walking speed

Distance (d) is calculated as:

`d = speed * time`

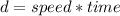
For Elvira, we have:

`d_E = s_E * 1/2`

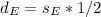
For Aletheia, we have:

`d_A = s_A * 2/3`

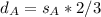
So, we have:

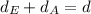`d_E + d_A = d` --- total distance

This gives:

`s_E * 1/2 + s_A * 2/3 = 3.2`

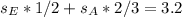
Recall that:

`s_E - s_A = 0.6`

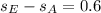
Make sE the subject

`s_E = 0.6+s_A`

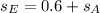
Substitute
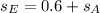`s_E = 0.6+s_A` in
`s_E * 1/2 + s_A * 2/3 = 3.2`

`(0.6+s_A)* 1/2 + s_A * 2/3 = 3.2`

`0.3+1/2s_A + 2/3s_A = 3.2`

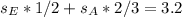
Collect like terms

`1/2s_A + 2/3s_A = 3.2-0.3`

`1/2s_A + 2/3s_A = 2.9`

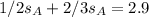
Express all as decimal

`0.5s_A + 0.7s_A= 2.9`

`1.2s_A= 2.9`

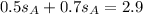
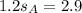
Divide both sides by 1.2

`s_A = 2.4`

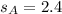
Recall that:

`s_E = 0.6+s_A`

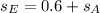
So, we have:

`s_E = 0.6+2.4`

`s_E = 3.0`