Answer:
17cm
Explanation:
Given that the Volume of a cone is 4,000 cm³. And we need to determine the height of the cone , if the diameter is 30cm .
Diagram :-
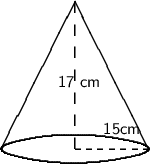
Step 1: Using the formula of cone :-
The volume of cone is ,
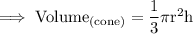
Step 2: Substitute the respective value :-
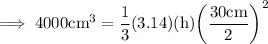
As Radius is half of diameter , therefore here r = 30cm/2 = 15cm .
Step 3: Simplify the RHS :-
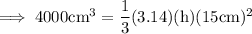
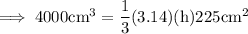
Step 4: Move all the constant nos. to one side
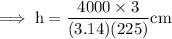
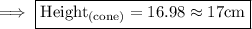
Hence the height of the cone is 17cm .