Question

A heat rate of 3 kW is conducted through a section of an insulating materials of cross-sectional area 10 m^2 and thickness 2.5 cm. If the inner (hot) surface temperature is 415°C and the thermal conductivity of the material is 0.2 W/m*k , what is the outer surface temperature?

Answer 1

Answer: The outer surface temperature is
`377.5^(o)C`.

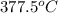Step-by-step explanation:

Given: Heat = 3 kW (1 kW = 1000 W) = 3000 W

Area = 10
`m^(2)`

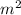
Length = 2.5 cm (1 cm = 0.01 m) = 0.025 m

Thermal conductivity = 0.2 W/m K

Temperature (inner) =
`415^(o)C`

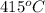
Formula used is as follows.

`q = KA ((t_(in) - t_(out)))/(L)`

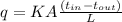
where,

K = thermal conductivity

A = area

L = length

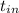`t_(in)` = inner surface temperature

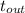`t_(out)` = outer surface temperature

Substitute the values into above formula as follows.

`q = KA ((t_(in) - t_(out)))/(L)\\3000 W = 0.2 * 10 * (415 - t_(out))/(0.025 m)\\t_(out) = 377.5^(o)C`

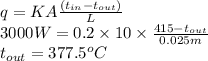
Thus, we can conclude that the outer surface temperature is
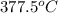`377.5^(o)C`.