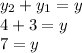Answer:
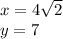
Explanation:
In order to solve this problem, the easiest approach is to draw a line connecting the vertex between the side with a measure of (y) and (3) to the side with the length (x). This side should be parallel to the side with a length of (4).
Since the new side constructed (call this side (b)), is parallel to the side with a length of (4) and is intersected by segments that are perpendicular to the side with a length of (4), the side (b) and (4) must have the same measure. Therefore (b = 4).
The triangle formed with sides (x) and (b) is a (45 - 45 - 90) triangle. Meaning that its angles have the following measure, (45 - 45- 90). This means that its sides follow the following ratio:
angle : side opposite
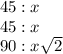
Apply this logic to the given situation.
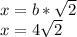
The side (b) divides the side (y) into two parts. Call the part that is a side of the triangle (
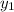 ) the side that is a part of the rectangle is called (
) the side that is a part of the rectangle is called (
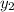 ). As per the logic used to find the lengths of side (b), one can use similar logic to find the length of side (
). As per the logic used to find the lengths of side (b), one can use similar logic to find the length of side (
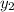 ). The sides (
). The sides (
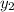 ) and (3) are parallel and are intersected by the sides with a measure of (4) and (b), therefore (
) and (3) are parallel and are intersected by the sides with a measure of (4) and (b), therefore (
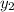 ) and (3) are cognrunet. Thus (
) and (3) are cognrunet. Thus (
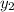 = 3).
= 3).
The base angles converse theorem states that when two angles in a triangle are congruent, the triangle is isosceles, and the sides opposite the congruent angles are also congruent. Thus, one can state the following:
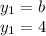
Now add up the measurement of (
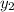 ) and (
) and (
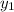 ) to find the measure of (y):
) to find the measure of (y):