Solution :
Given :
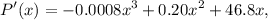 for x ≤ 200
for x ≤ 200
Total profit when 120 members are enrolled is :
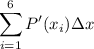 with
with
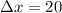
Using the left end points, we get,
The values of
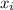 are : { 0, 20, 40, 60, 80, 100}
are : { 0, 20, 40, 60, 80, 100}
Therefore,
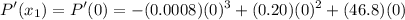
= 0
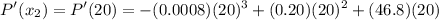
= 1009.6
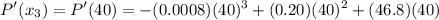
= 2140.8
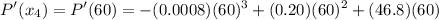
= 3355.2

= 4614.4
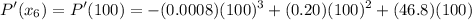
= 5880
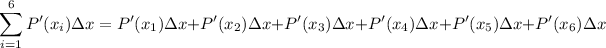
= (0)(20) + (1009.6)(20) + (2140.8)(20) + (3355.2)(20) + (4614.4)(20) + (5880)(20)
= (20)( 0 + 1009.6 + 2140.8 + 3355.2 + 4614.4 + 5880)
= (20)(17,000)
= 340,000 cents
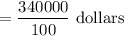
= 3400 dollars
Hence, the required total profit is 3400 dollars.