Question

In circle B, given isosceles triangle BTX, BA ⟂ WX, and WX = 10, what is the radius of circle B rounded to the nearest whole number?

Answer 1

We observe that :

`$\overline {BA} \perp \overline {WX}$`

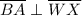
But BA is the perpendicular.

From the center B and WX is a chord.

Therefore, TW = TX (perpendicular from the centre of a circle to a chord bisects it)

Consider Δ BTX,

∠BTX = 90° (BA ⊥ WX)

BT = XT (Δ BTX is isosceles)

Since the angles opposite to equal sides are equal of a triangle arc are equal.

∠BTX = ∠BXT

But in the triangle,

∠TBX + ∠TXB + ∠BTX = 180°

∠TBX + ∠TBX + 90° = 180°

2 ∠TBX = 90°

∠TBX = 45°

From trigonometry, we get

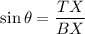`$\sin \theta =(TX)/(BX)$` ...............(1)

WX = 10

i.e., TX + TW = 10

But TX = TW

2 TX = 10

Tx = 5

BX = radius of circle.

∴
`$\sin 45^\circ = (5)/(BX)$`

`$(1)/(\sqrt2) = (5)/(BX)$`

`$BX = 5\sqrt2$`

`$=5 * 1.41$`

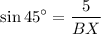
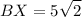
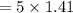
= 7

Therefore, the radius of the circle is 7 units.