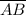Answer:
G is the midpoint of the side
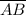 of triangle ΔOAB
of triangle ΔOAB
Explanation:
The vertices of the triangle ΔOAB are A(-15, 0), B(0, 8), and C(0, 0)
The coordinates of the point G = (-7.5, 4)
The length from the point A to the point G,
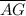 is given as follows;
is given as follows;
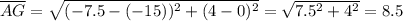
The length from the point A to the point B,
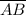 is given as follows;
is given as follows;
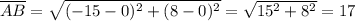
Therefore, the point G is the half way mark of
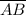 = The midpoint of the side
= The midpoint of the side