Question

!!kinda urgent!!

You decide to put $150 in a savings account to save for a $3,000 down payment on a new car. If the account has an interest rate of 2.5% per year and is compounded monthly, how long does it take you to earn $3,000 without depositing any additional funds?

Answer 1

119.95 years

Explanation:

The general equation is given by:

`P = A*(1 + (r)/(n) )^(n*t)`

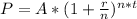
Where:

A is the initial amount, we know that the first deposit is of $150, then:

A = $150

t is the variable, in this case, is the number of years.

n = number of times that the interest is compounded in one unit of t, because the interest is compounded monthly, we have n = 12.

r = interest rate in decimal form.

r = 2.5%/100% = 0.025

Replacing these in our equation, we get that:

`P = 150*(1 + (0.025)/(12) )^(12*t)`

Now we want to find the time such that his savings, P, are equal to $3000.

Then we need to solve the equation:

`P = 150*(1 + (0.025)/(12) )^(12*t) = 3000`

`(1 + (0.025)/(12) )^(12*t) = 3000/150 = 20\\`

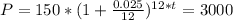
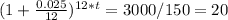
Now, remember that:

Ln(a^x) = x*ln(a)

So if we apply the natural logarithm to bot sides, we get:

`Ln((1 + (0.025)/(12) )^(12*t)) = Ln( 20)\\\\(12*t)*Ln(1 + (0.025)/(12)) = Ln(20)\\\\t = (Ln(20))/(12*Ln(1 + (0.025)/(12))) = 119.95`

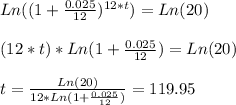
So after 119.95 years you will have the $3000.