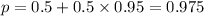Question

APP

A set of quiz scores has a mean of 78 and a standard
deviation of 9. Using a common grading scale where 60
and above is a passing score, what percentage of the
students passed this test?
Explain your answer in terms of the 68-95-99.7 rule.

Answer 1

The answer is "There are
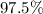`97.5\%` of the students pass in the test ".

Explanation:

Since a normally distributed random variable, the practical rule states:

About 68% of the metrics are in the 1 default deviation

About 95% of metrics correspond to 2 standard deviations from the average.

About 3 standard deviations of the average represent 99.7% of the measurement.

We have the following in this problem:

Average of 78, the average 9 default.

Calculating the percentage of students that passed the test.

`Above 60\\\\60 = 78 - 2* 9`

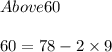
Therefore 60 is under the average for two standard deviations.

Its normality test is symmetric, so 50% of such observations are below mean and 50% below mean.

Everything was cleared of the 50 percent above.

Of the 50% below, 95% (within 2 known mean deviations) succeeded.

therefore

`p=0.5+0.5 * 0.95=0.975`