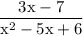Answer:
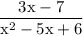
Explanation:
we would like to simplify the following:
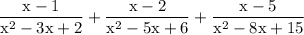
to simplify algebraic expression the first step is to figure out the LCM of the denominator in order to do so we can factor the denominators therefore factor the denominators and work out the LCM
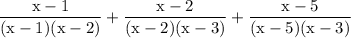
reduce fraction:
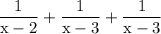
figure out the LCM and divide it by the denominator and multiply the result with the numerator which yields:
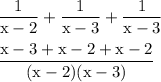
simplify addition:
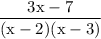
further expansion if necessary: