Question

Can someone help me with this math homework please!

Answer 1

3 Answers:

• Choice B
• Choice D
• Choice E

===============================================================

Step-by-step explanation:

Unfortunately your teacher is a bit vague here, but I'm assuming that the roots listed in the table are the only roots (and there aren't any other roots possible). If other roots were possible, then we'd have infinitely many possible answers and it would greatly muddy up the problem.

So we'll just stick to the basic assumption that the only roots are: -2, 0, and 2.

With that key assumption in mind, let's look at the answer choices to see which are true and which are false.

• A) False. This is because we see that f(x) = -15 when x = -3. Note how x = -3 is in the interval
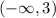  `(-\infty, 3)`. In other words, this is a counter example showing that f(x) > 0 is not the case when x is between -infinity and 3.
• B) True. Over the interval
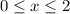  `0 \le x \le 2`, we have f(x) either equal to 0 or a negative value. For the interval 0 < x < 2, we would have f(x) < 0.
• C) False. The table shows that f(0) = 0 which means we aren't making f(x) < 0 to be the case.
• D) True. The table shows that if -2 < x < 0, then f(x) is positive. An example of this is f(-1) = 3 which is positive. The f(x) values in this region are above the x axis.
• E) True. We have f(x) either equal to 0 or something larger when
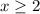  `x \ge 2` which translates over to the interval notation
  `[2, \infty)`

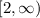
From that list above, we see that choices B, D and E are true.