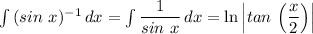Question

I need help with number 5

Answer 1

`\int\limits {{(sin \ x})^(-1) } \, dx = \text{ln}\left |{tan\, \left ((x)/(2) \right)} \right |`

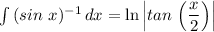
Explanation:

`\int\limits {(sin \ x)^(-1)} \, dx = \int\limits {(1)/(sin \ x) } \, dx`

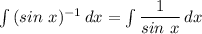
We have the following relationships;

`(1)/(sin \ x ) = csc \, x`

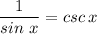
We can write;

`csc \, x = csc \, x * (csc \, x + cot \, x)/(csc \, x + cot \, x) = (csc^2 \, x + csc \, x \cdot cot \, x)/(csc \, x + cot \, x)`

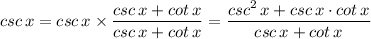
We note that the numerator of
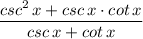`(csc^2 \, x + csc \, x \cdot cot \, x)/(csc \, x + cot \, x)` , which is
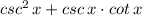`{csc^2 \, x + csc \, x \cdot cot \, x}` is the derivative of the denominator,
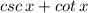`{csc \, x + cot \, x}`, therefore, we can use integration by substitution method and write;

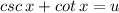`{csc \, x + cot \, x} = u`, from which we get;

`({csc^2 \, x + csc \, x \cdot cot \, x}) \cdot dx = (-1)du`

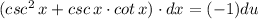
Therefore, we can write;

`\int\limits {(1)/(sin \ x) } \, dx = \int\limits {\frac{{csc^2 \, x + csc \, x \cdot cot \, x}}{{csc \, x + cot \, x}} } \, dx \Rightarrow -\int\limits {(1)/(u) } \, du = -ln \left |u \right |`

`\text{-ln} \left |u \right | = \text{-ln}\left |{csc \, x + cot \, x} \right |`

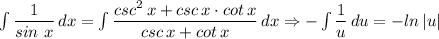
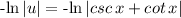
Therefore;

`\int\limits {(1)/(sin \ x) } \, dx = \text{-ln}\left |{csc \, x + cot \, x} \right |`

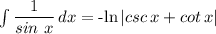
csc x + cot x = (1/sin x) + ((cos x)/(sin x)) = (1 + cos x)/(sin x)

(1 + cos x)/(sin x) = (cos²(x/2) + sin²(x/2) + cos²(x/2) - sin²(x/2))/(2sin(x/2)·cos(x/2)) = (2·cos²(x/2))/((2sin(x/2)·cos(x/2)) = cos(x/2)/sin(x/2) = cot(x/2)

Therefore;

`\text{-ln}\left |{csc \, x + cot \, x} \right | = \text{-ln}\left |{cot \, \left ((x)/(2) \right) } \right | = \text{ln}\left |{cot \, \left ((x)/(2) \right)} \right | ^(-1) = \text{ln}\left |{tan\, \left ((x)/(2) \right)} \right |`

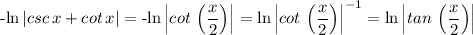
Therefore;

`\int\limits {{(sin \ x})^(-1) } \, dx = \int\limits {(1)/(sin \ x) } \, dx = \text{ln}\left |{tan\, \left ((x)/(2) \right)} \right |`