Question

The profit (in thousands of dollars) of a company is given by P(x) = -8x2 + 32x + 14.

Find the maximum profit of the company.
O a. 40 thousand dollars
O b. 45 thousand dollars
O c. 46 thousand dollars

Answer 1

C

Explanation:

The profit (in thousands of dollars) of a company is given by the function:

`\displaystyle P(x) = -8x^2+32x+14`

And we want to find the maximum profit of the company.

Since the function is a quadratic with a negative leading coefficient, the maximum profit will occur at its vertex. Recall that the vertex of a quadratic is given by:

`\displaystyle \text{Vertex} = \left(-(b)/(2a), f\left(-(b)/(2a)\right)\right)`

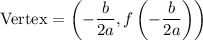
Find the x-coordinate of the vertex. In this case, a = -8, b = 32, and c = 14. Hence:

`\displaystyle x=-((32))/(2(-8))=(32)/(16)=2`

To find the maximum profit, substitute this value back into the function. Hence:

`\displaystyle P(2) = -8(2)^2+32(2) + 14 = 46`

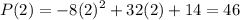
Therefore, the maximum profit of the company is 46 thousand dollars.

Our answer is C.