Given:
u varies directly with the square of p and inversely with d.
To find:
The equation for the given situation.
Solution:
If y is directly proportional to x, then
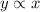
If y is inversely proportional to x, then

It is given that u varies directly with the square of p and inversely with d. So,
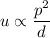
It can be written as:
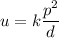
Where, k is the constant of proportionality.
Therefore, the required equation is
 .
.