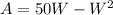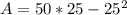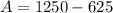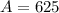Answer:
625 ft^2
Explanation:
Given
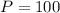 --- perimeter
--- perimeter
Required
The largest area
The perimeter is calculated as:
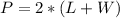
So, we have:
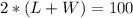
Divide both sides by 2

Make L the subject
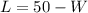
The area is calculated as:
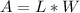
Substitute
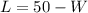

Open bracket
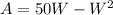
Differentiate with respect to W
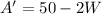
Set to 0; to get the maximum value of W

Collect like terms

Divide by -2

So, the maximum area is: