Question

Frogs are released into a pond where there are no other frogs of this species. The

function f(t) can be used to model the population of this new species after t years.
Below are 4 forms of the function that model this situation. Which form most clearly
shows the monthly population growth?

Answer 1

`f(t)=12(1.0139)^(12t)`

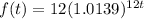
Explanation:

Let the initial number of frogs = 12

And their population is growing with the annual growth rate = 16.68% per year

Function modeling the population after 't' years will be,

`P(t)=12(1+r)^(t)`

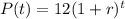
Here, r = Annual growth rate

t = Number of years

If we convert the annual growth rate to monthly growth rate,

Expression modeling the population will be,

`f(t)=12(1+(r)/(12))^(12t)`

`=12(1+(16.68)/(12))^(12t)`

`=12(1.0139)^(12t)`

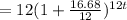
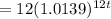
Therefore,
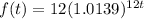`f(t)=12(1.0139)^(12t)` will be the answer.