Question

Suppose the group of 15 people consists of 7 men and 8 women. How many 6 person teams contain at most 3 men?

Answer 1

3850 of those 6 person teams contain at most 3 men.

Explanation:

The order in which the people are selected is not important, which means that the combinations formula is used to solve this question.

It drove 30.08 kilometers in an hour.

Combinations formula:

`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

0 men:

6 women from a set of 8. So

`C_(8,6) = (8!)/(2!6!) = 28`

1 men:

5 women from a set of 8

1 men from a set of 7. So

`C_(8,5)C_(7,1) = (8!)/(3!5!) * (7!)/(1!6!) = 392`

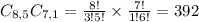
2 men:

4 women from a set of 8

2 men from a set of 7. So

`C_(8,4)C_(7,2) = (8!)/(4!4!) * (7!)/(2!5!) = 1470`

3 men:

3 women from a set of 8

3 men from a set of 7. So

`C_(8,3)C_(7,3) = (8!)/(5!3!) * (7!)/(3!4!) = 1960`

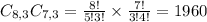
How many 6 person teams contain at most 3 men?

28 + 392 + 1470 + 1960 = 3850

3850 of those 6 person teams contain at most 3 men.