Answer:
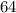
General Formulas and Concepts:
Calculus
Limits
Limit Rule [Variable Direct Substitution]:
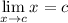
Limit Rule [Variable Direct Substitution Exponential]:
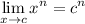
Limit Property [Multiplied Constant]:

Explanation:
Step 1: Define
Identify
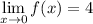
Step 2: Solve
- Rewrite [Limit Property - Multiplied Constant]:
![\displaystyle \lim_(x \to 0) (1)/(4)[f(x)]^4 = (1)/(4) \lim_(x \to 0) [f(x)]^4](https://img.qammunity.org/2022/formulas/mathematics/college/uxaq465qoeqdrpcfgcnx7b363lq3wa6wv0.png)
- Evaluate limit [Limit Rule - Variable Direct Substitution Exponential]:
![\displaystyle \lim_(x \to 0) (1)/(4)[f(x)]^4 = (1)/(4)(4^4)](https://img.qammunity.org/2022/formulas/mathematics/college/4om3qo565ivsb4czksqt2geg0qi0abkuhc.png)
- Simplify:
![\displaystyle \lim_(x \to 0) (1)/(4)[f(x)]^4 = 64](https://img.qammunity.org/2022/formulas/mathematics/college/2lbbj4ocv6hol3gkz1dmuqes17fpz764rt.png)
Topic: AP Calculus AB/BC (Calculus I/I + II)
Unit: Limits
Book: College Calculus 10e