Answer:
a.5005
b.
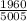
c.1/715
d.714/715
Explanation:
We are given that
Total men=8
Total women=7
Total people, n=8+7=15
r=6
a.
Combination formula:
Selection of r out of n people by total number of ways
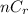
Using the formula
We have n=15
r=6
Total number of ways=
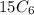
Total number of ways=
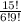
Using the formula
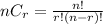
Total number of ways=
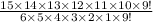
Total number of ways=5005
b. The probability of having exactly 3 men in the group
=
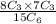
Using the formula
Probability,
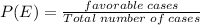
The probability of having exactly 3 men in the group=
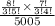
=
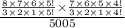
=
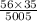
The probability of having exactly 3 men in the group
=
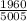
c. The probability of all the selected people in the group are women
=
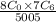
The probability of all the selected people in the group are women
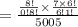
The probability of all the selected people in the group are women

d. The probability of having at least one man in the group
=1- probability of all the selected people in group are women
The probability of having at least one man in the group
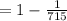
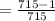

The probability of having at least one man in the group
