Answer:
1028 slits/mm
Step-by-step explanation:
We are given that
Wavelength of light,
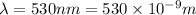
1nm=
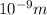

n=1
We have to find the number of slits per mm are marked on the grating.
We know that
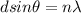
Using the formula
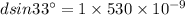
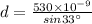

1m=
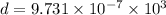 mm
mm
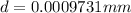
Number of slits=
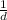
Number of slits=
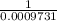 /mm
/mm
Number of slits=1028/mm
Hence, 1028 slits/mm are marked on the grating.