Answer:
23) No
24) No
25) Yes
Explanation:
Question 23)
We want to determine if a zero exists between 1 and 2 for the function:
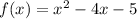
Find the zeros of the function. We can factor:

Zero Product Property:
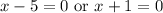
Solve for each case. Hence:
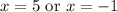
Therefore, our zeros are at x = 5 and x = -1.
In conclusion, a zero does not exist between 1 and 2.
Question 24)
We have the function:
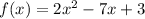
And we want to determine if a zero exists between 1 and 2.
Factor. We want to find two numbers that multiply to (2)(3) = 6 and that add to -7.
-6 and -1 suffice. Hence:
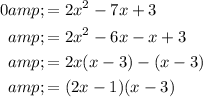
By the Zero Product Property:
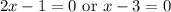
Solve for each case:
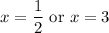
Therefore, our zeros are at x = 1/2 and x = 3.
In conclusion, a zero does not exist between 1 and 2.
Question 25)
We have the function:

And we want to determine if a zero exists between -2 and 3.
Factor. Again, we want to find two numbers that multiply to 3(-5) = -15 and that add to -2.
-5 and 3 works perfectly. Hence:

By the Zero Product Property:
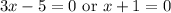
Solve for each case:
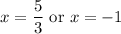
In conclusion, there indeed exists a zero between -2 and 3.