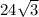Answer:
Explanation:
Let's just study that right triangle that is drawn inside the hexagon, shall we? That will make things tons easier for us. The area of this hexagon can be determined from the measurements we get from this right triangle. The area for the regular hexagon is:
where p is the perimeter of the hexagon (4 * 6 = 24) and a is the apothem. The apothem is also the same as the height of the right triangle we are going to work with.
Since the number of sides is 6 in this hexagon, we know that there are 6 angles originating from the center of the hexagon, and that each of these central angles measures 360/6 = 60 degrees. BUT the right triangle drawn for us has a vertex angle that is only half of 60. So if we pull out this right triangle, the top angle, the vertex angle, measures 30, making the other base angle a 60. So this is a 30-60-90 right triangle.
Here's what we have for this right triangle: the base of it is 2 (half of 4), the height of it is our unknown, and the other base angle is 60 degrees. The side across from the 30 degree angle is 2, so according to the Pythagorean triple for a 30-60-90 is x, x√3, and 2x. The value for the side across from the 60 degree is 2√3. That is also the value of our apothem. Now we are ready to fill in the formula:
so
A =
