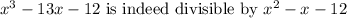Answer:
See Below.
Explanation:
We want to prove that:
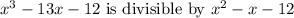
We can factor the divisor:
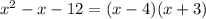
According to the Factor Theorem, if we have a polynomial P(x) divided by a binomial in the form of (x - a) and if P(a) = 0, then the binomial is a factor of P(x).
Our two binomial factors our (x - 4) and (x + 3). Thus, a = 4 and a = -3.
Evaluate the polynomial for both of these factors:
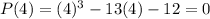
And:
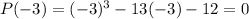
Since both yielded zero, the original polynomial is divisible by both (x - 4) and (x + 3) or x² - x - 12. Hence: