Question

Use the figure to find x.

Answer 1

`x = 8.57`

Explanation:

Here two triangles are given to us , which are attached to each other . Here we can use the concept of Trigonometry to find out the value of x. The angles of the triangle are 60° and 45° . Let the common side be p .

Step 1: Use the ratio of tan in upper triangle

`\rm\implies tan60^o = (perpendicular)/(base)`

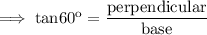
Substitute the respective values ,

`\rm\implies \sqrt3=(p)/(7)`

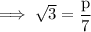
Cross multiply ,

`\rm\implies p = 7\sqrt3`

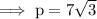
Step 2: Use the ratio of cos in lower triangle

`\rm\implies cos45^o = (base)/(hypontenuse)`

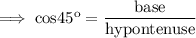
Substitute the respective values ,

`\rm\implies (1)/(\sqrt2)=(x)/(7\sqrt3)`

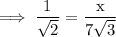
Cross multiply ,

`\rm\implies x= (7\sqrt3)/(\sqrt2)`

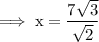
Put the approximate values of √2 and √3

`\rm\implies x= (7* 1.732)/(1.414)`

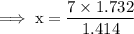
This equals to ,

`\rm\implies \boxed{\blue{\rm \quad x = 8.57\quad}}`

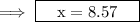
Hence the value of x is 8.57 .

Answer 2

The value of x is
`(7√(6))/(2)`

Solution given:

AB=7

BD=x

<BAC=60°

<DBC=45°

In right angled triangle ABC

Tan 60°=opposite/adjacent

Tan 60°=BC/AB

Substitute value

`√(3)`=
`(BC)/(7)`

BC=
`7√(3)`

again

againIn right angled triangle BCD

againIn right angled triangle BCDUsing Cos angle

Cos 45=adjacent/hypotenuse

Cos45°=BD/BC

Substituting value

`(√(2))/(2)=(x)/(7√(3))`

Doing criss cross multiplication

`(√(2))/(2)*7√(3)=x`

x=
`(7√(6))/(2)`