Question

A group of students is arranging squares into layers to create a project. The first layer has 6 squares. The second layer has 12 squares. Which formula represents an arithmetic explicit formula to determine the number of squares in each layer?

f(1) = 6; f(n) = 6 + d(n − 1), n > 0
f(1) = 6; f(n) = 6 ⋅ d(n − 1), n > 0
f(1) = 6; f(n) = 6 ⋅ d(n + 1), n > 0
f(1) = 6; f(n) = 6 + d(n + 1), n > 0

Answer 1

f(1) = 6; f(n) = 6 + d(n − 1), n > 0

Explanation:

I took the test on flvs and got it right.

100% Guaranteed Correct :)

, Hope this helps

Have a great day!!

Answer 2

a.

f(1)=6; f(n)=6+d(n-1), n>0

Explanation:

We are given that

First layer has squares, a=6

Second layer has squares, a2=12

We have to find an arithmetic explicit formula to determine the number of squares in each layer.

`d=a_2-a_1=12-6`

nth term of an A.P

`a_n=a+(n-1)d`

Substitute the value of a

Now, we get

`a_n=6+(n-1)d`

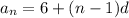
f(1)=a=6

`a_n=f(n)=6+d(n-1)`

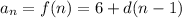
Hence, option a is correct.

a.

f(1)=6; f(n)=6+d(n-1), n>0