Answer:
d) The function ƒ(x) has a steeper slope than g(x)
Explanation:
We are given that
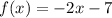
The graph g(x) passing through the point (1.2,0) and (0,4).
Let
y=f(x)=-2x-7
Slope of function f(x)
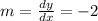
Slope formula
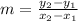
Using the formula
Slope of g(x)
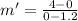
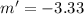
Slope of g(x)=-3.33<-2
Slope of f(x) is greater than slope of g(x).
Therefore, function f(x) has a steeper slope than g(x).
Option d) is correct.