Question

. When 2 moles of helium gas expand at constant pressure P = 1.0 × 105 Pascals, the temperature increases from 2℃ to 112℃. If the initial volume of the gas was 45 liters. Cp=20.8J/mol.K, Cv=12.6J/mol.K. Determine i. The work done W by the gas as it expands (4) ii. The total heat applied to the gas (2) iii. The change in internal energy (2

Answer 1

i. Work done by the gas as it expands is approximately 1,900 J

ii. The total heat supplied is approximately 4, 576 J

iii. The change in internal energy is approximately 2,772 J

Step-by-step explanation:

The constant pressure of the helium gas, P = 1.0 × 10⁵ Pa

The initial and final pressure of the gas, T₁, and T₂ = 2°C (275.15 K) and 112°C (385.15 K) respectively

The number of moles of helium in the sample of helium gas, n = 2 moles

The volume occupied by the gas at state 1, V₁ = 45 L

i. By ideal gas law, we have;

P·V = n·R·T

Therefore;

`V = (n \cdot R \cdot T)/(P)`

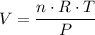
Plugging in the values gives;

`V_2 = (n \cdot R \cdot T_2)/(P)`

Where;

V₂ = The volume of the gas at state 2

Therefore;

`V_2 = (2 \cdot 8.314 \cdot 385.15)/(1.0 * 10^5) \approx 0.064`

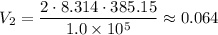
The volume of the gas at state 2, V₂ ≈ 0.064 m³ = 64 Liters

Work done by the gas as it expands, W = P × (V₂ - V₁)

∴ W ≈ 1.0 × 10⁵ Pa × (64 L - 45 L) = 1,900 J

Work done by the gas as it expands, W ≈ 1,900 J

ii. The total heat supplied, Q = Cp·n·ΔT

∴ Q = 20.8 J/(mol·K) × 2 moles × (385.15 K - 275.15 K) = 4,576 J

The total heat supplied, Q = 4, 576 J

iii. The change in internal energy, ΔU = Cv·n·ΔT

∴ ΔU = 12.6 J/(mol·K) × 2 moles × (385.15 K - 275.15 K) = 2,772 J

The change in internal energy, ΔU = 2,772 J