Question

In a set of 3 numbers the first is a positive integer, the second is 3 more than the first and the 3rd is a square of the second

a) the first number in the set is x. write the second and third numbers in terms of x

b) the sum of the numbers is 77

c) write down an equation in terms of x

d) show that your equation simplifies to x²+8x-65=0

​

Answer 1

Given:

In a set of 3 numbers the first is a positive integer, the second is 3 more than the first and the 3rd is a square of the second.

To find:

The equation for the given situation if the sum of the numbers is 77.

Solution:

a. Let the first number in the set is x.

The second is 3 more than the first. So, the second number is
`(x+3)`.

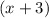The 3rd number is a square of the second. So, the third number is
`(x+3)^2`.

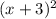Therefore, the first, second and third numbers are
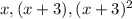`x,(x+3),(x+3)^2` respectively.

b. The sum of the numbers is 77.

First number + Second number + Third number = 77

c. So, the equation in terms of x is:

`x+(x+3)+(x+3)^2=77`

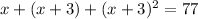
Therefore, the required equation is
`x+(x+3)+(x+3)^2=77`.

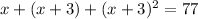d. On simplification, we get

`x+x+3+x^2+6x+9=77`
`[\because (a+b)^2=a^2+2ab+b^2]`

`x^2+(6x+x+x)+(3+9)=77`

`x^2+8x+12=77`

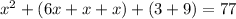
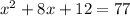
Subtract 77 from both sides.

`x^2+8x+12-77=77-77`

`x^2+8x-65=0`

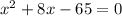
Therefore, the simplified form of the required equation is
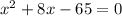`x^2+8x-65=0`.