Answer:
Number of oscillation = 106 oscillations
Step-by-step explanation:
Given the following data;
- Length = 2 m
- Acceleration due to gravity, g = 9.8 m/s²
- Time = 5 minutes
To find how many complete oscillations the pendulum makes in 5.00 min;
First of all, we would determine the period of oscillation of the pendulum using the following formula;
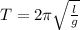
Where;
- T is the period.
- l is the length of the pendulum.
- g is acceleration due to gravity.
Substituting into the formula, we have;
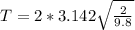

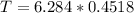
Period, T = 2.84 seconds
Next, we would determine the number of complete oscillation in 5 minutes;
We would have to convert the time in minutes to seconds.
Conversion:
1 minutes = 60 seconds
5 minutes = X seconds
Cross-multiplying, we have;
X = 5 * 60 = 300 seconds
Mathematically, the number of oscillation of a pendulum is given by the formula;
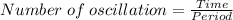
Substituting into the formula, we have;
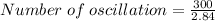
Number of oscillation = 105.63 ≈ 106 oscillations
Number of oscillation = 106 oscillations