Answer:
a) 0.3056 = 30.56% probability that 3 females and 2 males are selected.
b) 0.0306 = 3.06% probability that all five students selected are males.
c) 0.0131 = 1.31% probability that all five students selected are females.
d) 0.9869 = 98.69% probability that at least one male is selected.
Explanation:
The students are chosen from the sample without replacement, which means that the hypergeometric distribution is used to solve this question.
Hypergeometric distribution:
The probability of x successes is given by the following formula:
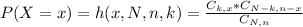
In which:
x is the number of successes.
N is the size of the population.
n is the size of the sample.
k is the total number of desired outcomes.
In this question:
15 + 13 = 28 students, which means that
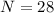
5 are selected, which means that
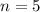
13 females, which means that
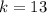
a. 3 females and 2 males are selected?
3 females, so this is P(X = 3).
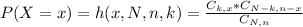
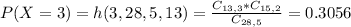
0.3056 = 30.56% probability that 3 females and 2 males are selected.
b.all five students selected are males?
0 females, so this is P(X = 0).
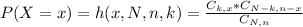
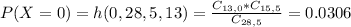
0.0306 = 3.06% probability that all five students selected are males.
c. all five students selected are females?
This is P(X = 5). So
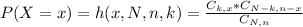
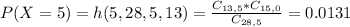
0.0131 = 1.31% probability that all five students selected are females.
d.at least one male is selected?
Less than five females, so:

0.9869 = 98.69% probability that at least one male is selected.