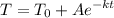Answer:
See Below.
Explanation:
We are given that:
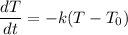
And we want to show that:
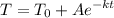
From the original equation, divide both sides by (T - T₀) and multiply both sides by dt. Hence:
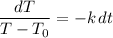
Take the integral of both sides:
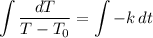
Integrate. For the left integral, we can use u-substitution. Note that T₀ is simply a constant. Hence:
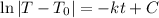
Raise both sides to e:
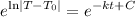
Simplify:
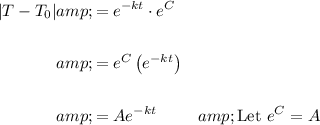
Since the temperature T will always be greater than or equal to the surrounding medium T₀, we can remove the absolute value. Hence:
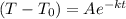
Therefore: