Question

Help with numer 5 please. thank you​

Answer 1

See Below.

Explanation:

We are given that:

`\displaystyle I = I_0 e^(-kt)`

Where I₀ and k are constants.

And we want to prove that:

`\displaystyle (dI)/(dt)+kI=0`

From the original equation, take the derivative of both sides with respect to t. Hence:

`\displaystyle (d)/(dt)\left[I\right] = (d)/(dt)\left[I_0e^(-kt)\right]`

Differentiate. Since I₀ is a constant:

`\displaystyle (dI)/(dt) = I_0\left((d)/(dt)\left[ e^(-kt)\right]\right)`

Using the chain rule:

`\displaystyle (dI)/(dt) = I_0\left(-ke^(-kt)\right) = -kI_0e^(-kt)`

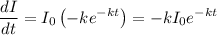
We have:

`\displaystyle (dI)/(dt)+kI=0`

Substitute:

`\displaystyle \left(-kI_0e^(-kt)\right) + k\left(I_0e^(-kt)\right) = 0`

Distribute and simplify:

`\displaystyle -kI_0e^(-kt) + kI_0e^(-kt) = 0 \stackrel{\checkmark}{=}0`

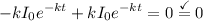
Hence proven.