Answer:
Explanation:
f(x)=-2x³+x-3
-f(x)=2x³-x+3
f(-x)=-2(-x)³+(-x)-3
=2x³-x-3
it is not equal to f(x) or -f(x)
so it is neither even or odd.
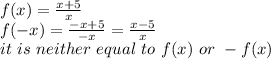
it is neither even or odd.
f(x)=x^4-x^2+10
f(-x)=(-x)^4-(-x)^2+10=x^4-x^2+10=f(x)
it is an even function.
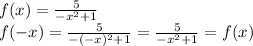
it is an even function.
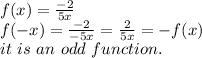
f(x)=x^9-x^5+4x^3
f(-x)=(-x)^9-(-x)^5+4(-x)^3
=-x^9+x^5-4x^3
=-(x^9-x^5+4x^3)
=-f(x)
it is an odd function.