Given:
The data set is:
9, 6, 8, 9, 7, 4, 3, 5, 2, 4
To find:
The mean absolute deviation (MAD) of the given data.
Solution:
We have,
9, 6, 8, 9, 7, 4, 3, 5, 2, 4
The mean of the given data set is:
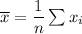
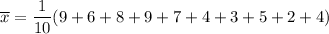
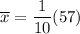
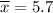
So, the mean of the given data set is 5.7.
The mean absolute deviation (MAD) is:
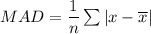
The mean absolute deviation (MAD) of the given data is:
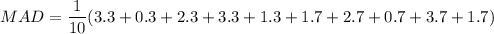
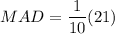

Therefore, the mean absolute deviation (MAD) of the given data set is 2.1.