Question

If you hit the surface of Iron with a photon of energy and find that the ejected electron has a wavelength of .75 nm, what is the wavelength of the incoming photon in nanometers?

Answer 1

The wavelength of the incoming photon is 172.8 nm

Step-by-step explanation:

The wavelength of the incoming photon can be calculated with the photoelectric equation:

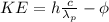`KE = h(c)/(\lambda_(p)) - \phi` (1)

Where:

KE: is the kinetic energy of the electron

h: is Planck's constant = 6.62x10⁻³⁴ J.s

c: is the speed of light = 3.00x10⁸ m/s

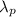`\lambda_(p)`: is the wavelength of the photon =?

Φ: is the work function of the surface (Iron) = 4.5 eV

The kinetic energy of the electron is given by:

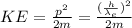`KE = (p^(2))/(2m) = (((h)/(\lambda_(e)))^(2))/(2m)` (2)

Where:

p: is the linear momentum = h/λ

m: is the electron's mass = 9.1x10⁻³¹ kg

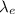`\lambda_(e)`: is the wavelength of the electron = 0.75 nm = 0.75x10⁻⁹ m

Hence, the wavelength of the photon is:

`(((h)/(\lambda_(e)))^(2))/(2m) = h(c)/(\lambda_(p)) - \phi`

`\lambda_(p) = (hc)/((h^(2))/(2m\lambda_(e)^(2)) + \phi) = (6.62 \cdot 10^(-34) J.s*3.00\cdot 10^(8) m/s)/(((6.62 \cdot 10^(-34) J.s)^(2))/(2*9.1 \cdot 10^(-31) kg*(0.75 \cdot 10^(-9) m)^(2)) + 4.5 eV*(1.602 \cdot 10^(-19) J)/(1 eV)) = 1.728 \cdot 10^(-7) m = 172.8 nm`

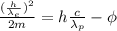
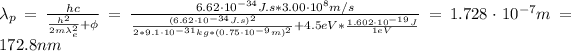
Therefore, the wavelength of the incoming photon is 172.8 nm.

I hope it helps you!