Question

here are the first five terms of a quadratic sequence (1 8, 21, 40, 65). the nth term of this sequence can be written in the form (an2 + bn). where a and b are integers. work out the value of a and the value of b

Answer 1

a=3 and b=-2

Explanation:

We are given that five terms of a quadratic sequence are

1 8, 21, 40, 65.

The nth term of this sequence

=
`an^2+bn`

We have to find the value of a and b where a and b are integers.

For n=1

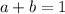`a+b=1` ......(1)

For n=2

`(2)^2a+2b=8`

`4a+2b=8`

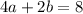
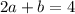`2a+b=4` .....(2)

Subtract equation (1) from (2) we get

`2a-a=4-1=3`

`a=3`

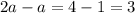
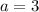
Using the value of a=3 in equation (1)

`3+b=1`

`b=1-3=-2`

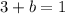
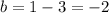
Hence, the value of

a=3 and b=-2