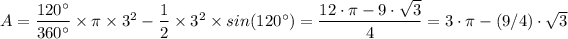Question

12 120° 3 3 Fig. 12.51 Calculate the area of the shaded segment in Fig. 12.51. (Leave your answer in terms of .) [JAMB]​

Answer 1

`\text {The \ area \ of \ the \ shaded \ segment, A} = 3 \cdot \pi - (9)/(4) \cdot √(3)`

Explanation:

The details of the circle that has the shaded segment, and the segment are;

The radius of the circle, r = 3

The angle of the arc of the segment, θ = 120°

The area of a segment, A, is given as follows;

`A = (\theta)/(360^(\circ)) * \pi * r^2 - (1)/(2) * r^2 * sin(\theta)`

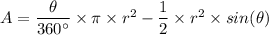
The area of the given segment is therefore;

`A = (120^(\circ))/(360^(\circ)) * \pi * 3^2 - (1)/(2) * 3^2 * sin(120^(\circ)) = (12\cdot \pi-9\cdot √(3) )/(4) = 3\cdot \pi - (9/4)\cdot √(3)`